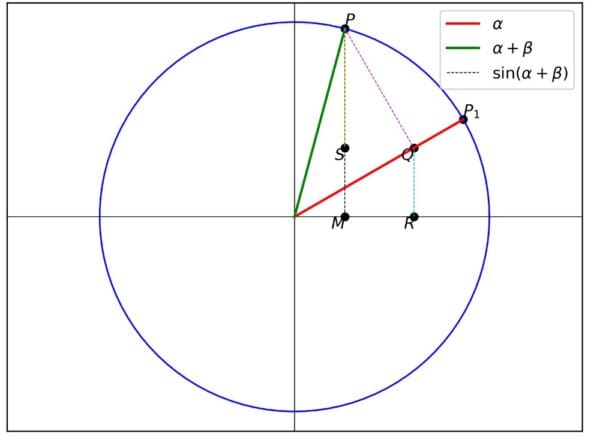
使用單位圓與三角函數線法
1. 構建圖形
在平面直角坐標系中作單位圓 $O$(圓心在原點,半徑 $r = 1$)。設角 $\alpha$、$\beta$ 均為任意角,角 $\alpha$ 的終邊與單位圓交於點 $P_1$,角 $\beta$ 以角 $\alpha$ 的終邊為始邊,其終邊與單位圓交於點 $P$,那麼角 $\alpha + \beta$ 的終邊就是 $OP$。
過點 $P$ 作 $PM\perp x$ 軸於點 $M$,則 $\sin(\alpha + \beta)=MP$(根據正弦函數的定義:在單位圓中,角的正弦值等於其終邊與單位圓交點的縱坐標)。
過點 $P$ 作 $PQ\perp OP_1$ 於點 $Q$,過點 $Q$ 作 $QR\perp x$ 軸於點 $R$,過點 $P$ 作 $PS\perp QR$ 交 $QR$ 的延長線於點 $S$。
2. 角度與線段關係分析
- 因為 $OP = 1$,在 $Rt\triangle OPQ$ 中,$\angle POQ=\beta$,根據三角函數定義:
- $OQ = \cos\beta$,$QP = \sin\beta$。
- 觀察圖形可知,$\angle QPS=\alpha$(因為 $PQ\perp OP_1$,$PS\perp QR$,$QR\perp x$ 軸,通過角度的等量代換可得)。
3. 線段分解與推導
我們知道 $MP = SR + PS$。
-
- 計算 $SR$:
由於 $SR = QN$(矩形對邊相等,四邊形 $QNMS$ 是矩形),在 $Rt\triangle OQN$ 中,$\angle QON = \alpha$,$OQ=\cos\beta$,根據正弦函數定義可得 $QN = OQ\sin\alpha$,所以 $SR=\cos\beta\sin\alpha$。
-
- 計算 $PS$:
在 $Rt\triangle PQS$ 中,$\angle QPS=\alpha$,$QP = \sin\beta$,根據餘弦函數定義可得 $PS = QP\cos\alpha=\sin\beta\cos\alpha$。
4. 得出結論
因為 $MP = SR + PS$,把 $SR=\cos\beta\sin\alpha$ 和 $PS=\sin\beta\cos\alpha$ 代入可得:
$\sin(\alpha + \beta)=MP=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
綜上,利用單位圓和三角函數線,成功證明了兩角和的正弦公式 $\sin(\alpha + \beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$。
例子一**:求$\sin75^{\circ}$的值。
– 因為\(75^{\circ}=45^{\circ} + 30^{\circ}\),令\(\alpha = 45^{\circ}\),\(\beta = 30^{\circ}\)。
– 根據正弦和角公式\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\),且\(\sin45^{\circ}=\frac{\sqrt{2}}{2}\),\(\cos45^{\circ}=\frac{\sqrt{2}}{2}\),\(\sin30^{\circ}=\frac{1}{2}\),\(\cos30^{\circ}=\frac{\sqrt{3}}{2}\)。
– 則\(\sin75^{\circ}=\sin(45^{\circ}+30^{\circ})=\sin45^{\circ}\cos30^{\circ}+\cos45^{\circ}\sin30^{\circ}\)
– 把值代入可得:\(\sin75^{\circ}=\frac{\sqrt{2}}{2}\times\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\times\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}\)。
**例子二**:已知\(\sin\alpha=\frac{3}{5}\),\(\alpha\in(0,\frac{\pi}{2})\),\(\cos\beta =-\frac{12}{13}\),\(\beta\in(\frac{\pi}{2},\pi)\),求\(\sin(\alpha + \beta)\)的值。
– 首先,根據\(\sin^{2}\alpha+\cos^{2}\alpha = 1\),因為\(\sin\alpha=\frac{3}{5}\),\(\alpha\in(0,\frac{\pi}{2})\),所以\(\cos\alpha=\sqrt{1 – \sin^{2}\alpha}=\sqrt{1 – (\frac{3}{5})^{2}}=\sqrt{1-\frac{9}{25}}=\sqrt{\frac{16}{25}}=\frac{4}{5}\)。
– 其次,根據\(\sin^{2}\beta+\cos^{2}\beta = 1\),因為\(\cos\beta =-\frac{12}{13}\),\(\beta\in(\frac{\pi}{2},\pi)\),所以\(\sin\beta=\sqrt{1-\cos^{2}\beta}=\sqrt{1 – (-\frac{12}{13})^{2}}=\sqrt{1-\frac{144}{169}}=\sqrt{\frac{25}{169}}=\frac{5}{13}\)。
– 然後,根據正弦和角公式\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)。
– 把\(\sin\alpha=\frac{3}{5}\),\(\cos\alpha=\frac{4}{5}\),\(\cos\beta =-\frac{12}{13}\),\(\sin\beta=\frac{5}{13}\)代入可得:
– \(\sin(\alpha + \beta)=\frac{3}{5}\times(-\frac{12}{13})+\frac{4}{5}\times\frac{5}{13}=\frac{-36 + 20}{65}=-\frac{16}{65}\)。