這個定理在解決三角形問題時非常有用,尤其在已知邊長和角度時,可以方便地求出其他未知量。
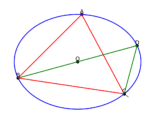
方法一:藉助外接圓和直角三角形性質
- 作$\triangle ABC$的外接圓$O$,連接$BO$並延長交圓於$D$,再連$CD$。
- 由於$BD$是直徑,所以$\angle BCD = 90^{\circ}$ ,且$\angle A = \angle D$(同弧圓周角相等)。
- 在$Rt\triangle BCD$中,$\sin D=\frac{BC}{BD}$,已知$BC = a$,$BD = 2R$($R$為外接圓半徑),因$\angle A = \angle D$,則$\sin A=\sin D=\frac{a}{2R}$,即$\frac{a}{\sin A}=2R$。
- 同理,通過類似輔助線做法可證$\frac{b}{\sin B}=2R$和$\frac{c}{\sin C}=2R$ 。
綜上,$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。
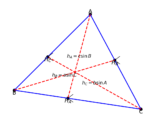
方法二:利用三角形面積公式
- 已知$S_{\triangle ABC}=\frac{1}{2}ah_a$ ,從$A$作$BC$邊上高$AD$,$AD = c\sin B$,所以$S_{\triangle ABC}=\frac{1}{2}ac\sin B$。同理可得$S_{\triangle ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A$。
- 由$\frac{1}{2}ac\sin B=\frac{1}{2}ab\sin C$,約去$\frac{1}{2}a$得$c\sin B = b\sin C$,即$\frac{b}{\sin B}=\frac{c}{\sin C}$;由$\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A$,約去$\frac{1}{2}b$得$a\sin C = c\sin A$,即$\frac{a}{\sin A}=\frac{c}{\sin C}$ 。
- 結合方法一中$\frac{a}{\sin A}=2R$,可得$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。
綜上,通過這兩種常見方法可證$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$。