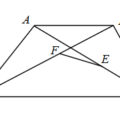
<多選>假設\(A\),\(B\)為一拋物線\(\Gamma\)上兩點且其連線段通過\(\Gamma\)的焦點\(F\) 。設\(A\),\(F\),\(B\)在\(\Gamma\)之準線上的投影分別為\(A’\) ,\(F’\) ,\(B’\) 。試選出等於\(\frac{\overline{A’F’}}{\overline{A’A}}\)的選項。
(注意:此示意圖僅說明各點的相關位置,各點間距離關係並不正確)

(1)\(\tan\angle1\),其中\(\angle1=\angle A’F’A\)
(2)\(\sin\angle2\),其中\(\angle2=\angle AF’F\)
(3)\(\sin\angle3\),其中\(\angle3=\angle A’AF\)
(4)\(\cos\angle4\),其中\(\angle4=\angle F’FB\)
(5)\(\tan\angle5\),其中\(\angle5=\angle FF’B\)
### 解析
(1) ×:
\(\triangle AA'F'\) 是直角三角形,故 \(\frac{\overline{A'F'}}{\overline{AA'}} = \frac{1}{\tan\angle 1}\)。
(2) ×:
由內錯角相等,\(\angle 2 = \angle AF'F = \angle A'AF\),因此 \(\tan\angle 2 = \frac{\overline{A'F'}}{\overline{AA'}}\)。
(3) ○:
如圖,\(\overline{AF} = \overline{AA'}\) 且 \(\overline{FH} = \overline{A'F'}\),故 \(\sin\angle 3 = \frac{\overline{FH}}{\overline{AF}} = \frac{\overline{A'F'}}{\overline{AA'}}\)。
(4) ×:
由同位角相等,\(\angle 4 = \angle 3\),但 \(\frac{\overline{A'F'}}{\overline{AA'}} = \sin\angle 3 = \sin\angle 4\) 的推導不符合題意要求。
(5) ○:
由內錯角相等,\(\angle 5 = \angle FF'B = \angle F'BB'\);
根據拋物線定義,\(\overline{BB'} = \overline{BF}\),故 \(\tan\angle 5 = \frac{\overline{B'F'}}{\overline{BB'}} = \frac{\overline{B'F'}}{\overline{BF}}\);
又 \(\frac{\overline{B'F'}}{\overline{BF}} = \frac{\overline{F'A'}}{\overline{FA}} = \frac{\overline{F'A'}}{\overline{AA'}}\)。
最終選:(3)(5)