111分科數學甲試題-12

---

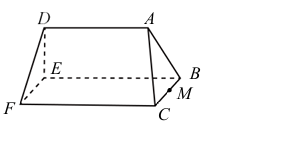
<非選擇>有一積木，其中\(ACFD\)和\(ABED\)是兩個全等的等腰梯形，\(BCFE\)是一個矩形。設\(A\)點在直線\(BC\)的投影為\(M\)且在平面\(BCFE\)的投影為\(P\)。已知\(\overline{AD}=30\) ，\(\overline{CF}=40\) ，\(\overline{AP}=15\)且\(\overline{BC}=10\) 。將平面\(BCFE\)置於水平桌面上，且將與\(BCFE\)平行的平面稱為水平面。利用\(\overline{AD}\)在平面\(BCFE\)的投影長為\(30\)，可得\(\tan\angle AMP = \)__________ 。