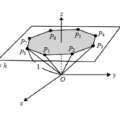
<非選擇題>坐標空間中,\(O(0,0,0)\)為原點。平面\(z = h\)(其中\(0≤h≤1\))上有一以\((0,0,h)\)為圓心的圓,在此圓上依逆時針順序取8點構成正八邊形\(P_0P_1P_2P_3P_4P_5P_6P_7\),使得各線段\(\overline{OP_j}(0≤j≤7)\)的長度都是1。在\(\overrightarrow{OP_0}\)和\(\overrightarrow{OP_4}\)夾角不超過\(90^{\circ}\)的條件下,試問正八角錐體積\(V(h)\)的最大值為何?(6分)
已知條件:
1. \( \sqrt{1-h^2} \geq 0 \implies 0 \leq h \leq 1 \);
2. \( \overrightarrow{OP_1} \cdot \overrightarrow{OP_2} = 2h^2 - 1 \geq 0 \)(夾角不超過 \( 90^\circ \)),故 \( h \geq \frac{1}{\sqrt{2}} \)。
由①②得 \( \boxed{\frac{1}{\sqrt{2}} \leq h \leq 1} \)。
設體積函數 \( V(h) \),其導數為 \( V'(h) = \frac{2\sqrt{2}}{3}(1 - 3h^2) \),令 \( V'(h)=0 \),得 \( h = \pm \frac{1}{\sqrt{3}} \)(均不在區間 \( \left[\frac{1}{\sqrt{2}}, 1\right] \) 內,故無臨界點)。
因此體積最大值出現在區間端點 \( h = \frac{1}{\sqrt{2}} \) 處:
\[
V\left(\frac{1}{\sqrt{2}}\right) = \frac{2\sqrt{2}}{3} \times \left( \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{4} \right) = \frac{2\sqrt{2}}{3} \times \frac{\sqrt{2}}{4} = \frac{1}{3}
\]
故最大體積為 \( \boxed{\frac{1}{3}} \)。