<非選擇題>
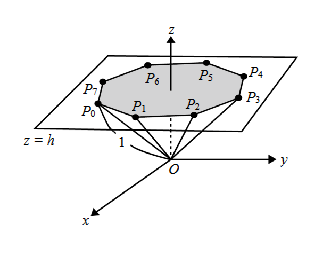
坐標空間中,\(O(0,0,0)\)為原點。平面\(z = h\)(其中\(0\leq h\leq1\))上有一以\((0,0,h)\)為圓心的圓,在此圓上依逆時針順序取8點構成正八邊形\(P_0P_1P_2P_3P_4P_5P_6P_7\),使得各線段\(\overline{OP_j}(0\leq j\leq7)\)的長度都是1。試以\(h\)表示向量內積\(\overrightarrow{OP_0}\cdot\overrightarrow{OP_4}\)。(4分)
在平面\(z = h\)上,以\((0,0,h)\)為圓心,半徑\(r=\sqrt{1 - h^{2}}\)(由\(\vert\overrightarrow{OP_j}\vert = 1\),根據勾股定理可得)。
將正八邊形放置在平面\(z = h\)上,以圓心\((0,0,h)\)為中心建立平面直角坐標系(在\(z = h\)這個平面內)。
對於正八邊形,相鄰兩邊夾角為\(\frac{360^{\circ}}{8}=45^{\circ}\),\(\overrightarrow{OP_0}\)與\(\overrightarrow{OP_4}\)的夾角為\(4\times45^{\circ}=180^{\circ}\)。
設\(\overrightarrow{OP_0}=(x_1,y_1,h)\),\(\overrightarrow{OP_4}=(x_2,y_2,h)\),由\(\vert\overrightarrow{OP_0}\vert=\vert\overrightarrow{OP_4}\vert = 1\),可得\(x_1^{2}+y_1^{2}+h^{2}=1\),\(x_2^{2}+y_2^{2}+h^{2}=1\)。
\(\overrightarrow{OP_0}\cdot\overrightarrow{OP_4}=x_1x_2 + y_1y_2+h^{2}\)。
在平面\(z = h\)上,\(\overrightarrow{OP_0}\)與\(\overrightarrow{OP_4}\)的向量關係可根據正八邊形的旋轉性質得到。
由正八邊形性質可知,\(\overrightarrow{OP_0}\)與\(\overrightarrow{OP_4}\)在\(z = h\)平面上的投影向量大小相等,方向相反(夾角\(180^{\circ}\)),且投影向量模長\(r=\sqrt{1 - h^{2}}\)。
所以\(\overrightarrow{OP_0}\cdot\overrightarrow{OP_4}=- (1 - h^{2})+h^{2}=2h^{2}-1\)。