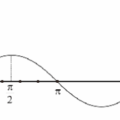
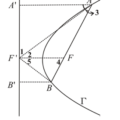
<多選>坐 標 平 面 上,考 慮 兩 函 數 \( f (x) = x^{5}-5x^{3}+5x^{2}+5\) 與 \( g(x)=\sin(\frac{\pi}{3}x+\frac{\pi}{2})\) 的 函 數 圖 形（其中 \( \pi \) 為圓周率）。試 選 出 正 確 的 選 項。
(1) \( f'(1) = 0\)
(2) \( y = f (x) \) 在 閉 區 間 \([0,2]\) 為遞增
(3) \( y = f (x) \) 在 閉 區 間 \([0,2]\) 為凹向上
(4) 對 任 意 實 數 \( x\),\( g(x + 6\pi) = g(x)\)
(5) \( y = f (x) \) 與 \( y = g(x) \) 在 閉 區 間 \([3,4]\) 皆為遞增
答案
(1) \(f'(x)=5x^{4}-15x^{2}+10x\),\(f'(1)=5 - 15 + 10 = 0\),(1) 對；
(2) \(f'(x)=5x(x^{3}-3x + 2)=5x(x - 1)^{2}(x + 2)\),在 \([0,2]\) 上 \(f'(x)\geq0\),\(y = f (x)\) 遞增,(2) 對；
(3) \(f''(x)=20x^{3}-30x + 10\),在 \([0,2]\) 上 \(f''(x)\) 有正有負,不是凹向上,(3) 錯；
(4) \(g(x)=\sin(\frac{\pi}{3}x)\) 的周期 \(T=\frac{2\pi}{\frac{\pi}{3}} = 6\),不是 \(6\pi\),(4) 錯；
(5) \(f'(x)>0\) 在 \([3,4]\) 成立,
$g(x)週期6且x=3時\theta=\frac{\pi}{3}\times3+\frac{\pi}{2}=\frac{3}{2}\pi,\\x=4時\theta=\frac{\pi}{3}\times4+\frac{\pi}{2}=\frac{11}{6}\pi,此區間g(x)遞增,(5)對。$
答案是(1)(2)(5)。 報錯
ChatGPT DeepSeek
相關試題
