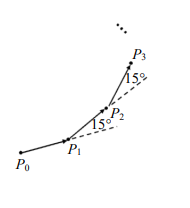
<選填>如圖所示，平面上有一點 \( P_0 \) 先朝某方向前進 2 個單位長到達點 \( P_1 \) 後，依前進方向左轉 15 度；朝新方向前進 2 個單位長到達點 \( P_2 \) 後，然後再依前進方向左轉 15 度；再朝新方向前進 2 個單位長到達點 \( P_3 \) 後，…依此類推。則向量 \( \overrightarrow{P_2P_3} \) 與 \( \overrightarrow{P_5P_6} \) 的內積為 __________（化為最簡根式）。
答案
1. 分析向量長度：
由題意，每段向量 \( \overrightarrow{P_nP_{n+1}} \) 的長度均為 2，即 \( |\overrightarrow{P_2P_3}| = 2 \)，\( |\overrightarrow{P_5P_6}| = 2 \)。
2. 分析向量夾角：
每次左轉 \( 15^\circ \)，故 \( \overrightarrow{P_2P_3} \) 與 \( \overrightarrow{P_5P_6} \) 的夾角為 \( 3 \times 15^\circ = 45^\circ \)。
3. 計算向量內積：
向量內積公式為 \( \vec{u} \cdot \vec{v} = |\vec{u}||\vec{v}|\cos\theta \)，代入得：
\[
\overrightarrow{P_2P_3} \cdot \overrightarrow{P_5P_6} = 2 \times 2 \times \cos45^\circ = 4 \times \frac{\sqrt{2}}{2} = 2\sqrt{2}
\] 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf
相關試題
