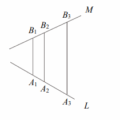
<非選擇>18-20 題為題組
空地上有三根與地面垂直且等高的電線桿,其底座在一直線上且間距相等。某甲以單點透視法在畫布上畫這三根電線桿。在畫布上設坐標系,使得電線桿皆與\(y\)軸平行,三根底座的點分別為\(A_1(0,0)\)、\(A_2\)、\(A_3\),都在直線\(L:x + 3y = 0\)上；三根頂端的點分別為\(B_1(0,3)\)、\(B_2\)、\(B_3\),都在直線\(M:2x – 3y + 9 = 0\)上,如圖所示。已知\(A_3B_3 = 2A_1B_1\),且由單點透視法可知直線\(A_1B_3\)與直線\(A_3B_1\)的交點在直線\(A_2B_2\)上。設\(L\)和\(M\)相交於\(P\)點（此點又稱為「消失點」）。試求\(P\)與\(B_3\)這兩點的坐標。（非選擇題,\(6\)分）
1. 求\(P\)點坐標：
聯立直線\(L:x + 3y = 0\)與\(M:2x - 3y + 9 = 0\)的方程,將\(x = - 3y\)代入\(2x - 3y + 9 = 0\),得\(-6y - 3y + 9 = 0\),解得\(y = 1\),則\(x = - 3\),所以\(P(-3,1)\)。
2. 求\(B_3\)點坐標：
設\(A_3(x_0,y_0)\),因為\(A_3\)在\(L\)上,所以\(x_0 + 3y_0 = 0\),即\(x_0 = - 3y_0\)。\(A_1B_1 = 3\),\(A_3B_3 = 6\)。設\(B_3(x_1,y_1)\),\(B_3\)在\(M\)上,\(2x_1 - 3y_1 + 9 = 0\)。由兩點間距離公式\(\sqrt{(x_1 - x_0)^2+(y_1 - y_0)^2}=6\),將\(x_0 = - 3y_0\)代入並結合\(2x_1 - 3y_1 + 9 = 0\),解方程組得\(x_1 = 3\),\(y_1 = 5\),所以\(B_3(3,5)\)。綜上,\(P(-3,1)\),\(B_3(3,5)\)。 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf
相關試題
