112學測數學B試題-20

---

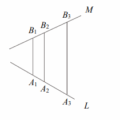
<非選擇>[18-20 題為題組]
空地上有三根與地面垂直且等高的電線桿,其底座在一直線上且間距相等。某甲以單點透視法在畫布上畫這三根電線桿。在畫布上設坐標系,使得電線桿皆與\(y\)軸平行,三根底座的點分別為\(A_1(0,0)\)、\(A_2\)、\(A_3\),都在直線\(L:x + 3y = 0\)上；三根頂端的點分別為\(B_1(0,3)\)、\(B_2\)、\(B_3\),都在直線\(M:2x – 3y + 9 = 0\)上,如圖所示。已知\(A_3B_3 = 2A_1B_1\),且由單點透視法可知直線\(A_1B_3\)與直線\(A_3B_1\)的交點在直線\(A_2B_2\)上。設\(L\)和\(M\)相交於\(P\)點（此點又稱為「消失點」）。若有隻蜜蜂恰好停在中間那根電線桿上距離底座與頂端的長度比為\(1:2\)的位置上。某甲想在這個畫布的線段\(A_2B_2\)上畫出這隻蜜蜂,假設畫布上蜜蜂位置為\(Q\)點,即點\(Q\)到線段\(A_2B_2\)的底座\(A_2\)與到線段\(A_2B_2\)頂端\(B_2\)的長度比為\(1:2\),試求\(Q\)點坐標。（非選擇題,\(6\)分）