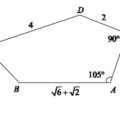
<非選擇>[題組說明18-20]
試求 ∆BCD 的面積。(非選擇題,4 分)
答案
$\begin{align*}
&【解法一】\overline{BC}邊上的高為\sqrt{9^2 - 4^2}=\sqrt{65},\\
&故\triangle BCD面積=\frac{1}{2}×8×\sqrt{65}=4\sqrt{65};\\
\\
&【另解(海龍公式)】半周長s=\frac{9+9+8}{2}=13,\\
&面積=\sqrt{s(s-9)(s-9)(s-8)}=\sqrt{13×4×4×5}=4\sqrt{65}。
\end{align*}$