---

<多選>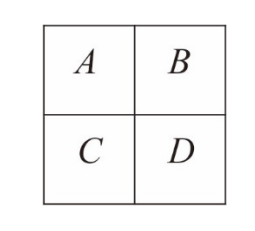小明寫了一個程式讓機器人在\(2×2\)的棋盤中移動,如圖所示。每執行一次,程式會選擇「上、下、左、右」中的某一個方向,不同方向被選擇的機率均相等,並指示機器人依該方向移動一格,但若選到的方向會跑出棋盤,則機器人該次會停在原地。每次執行都是從上次所在位置依程式重新選取的方向移動,假設機器人的初始位置在\(A\)。 令執行程式\(n\)次後,機器人停留在\(A\)、\(B\)、\(C\)、\(D\)的機率分別為\(a_n\)、\(b_n\)、\(c_n\)和\(d_n\)。試選出正確的選項。
(1) \(b_1 = \frac{1}{4}\)；
(2) \(b_2=\frac{1}{8}\)；
(3) \(a_2+d_2=\frac{3}{4}\)；
(4) \(b_{99}=c_{99}\)；
(5) \(a_{100} + d_{100} \gt\frac{ 1}{2}\)