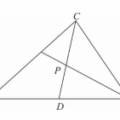
<選填>教室的某牆角是由牆面和地面兩兩互相垂直所構成。設牆角為點\(O\),現有一個三角形擋板\(ABC\),其中頂點\(A\)、\(B\)、\(C\)位在牆面間或牆面與地面間的交界線上,並與牆角\(O\)的距離分別為\(20\)、\(20\)、\(10\)公分；\(AB\)、\(BC\)、\(CA\)三邊與牆面或地面貼合,如圖所示。則\(\angle BAC = \underline{}\)（化為最簡根式）
答案
設
- \( A(20,0,0) \)、\( B(0,20,0) \)（在地面兩牆交線）
- \( C(0,0,10) \)（在牆上）
則
- \( \vec{AB} = (-20,20,0) \)
- \( \vec{AC} = (-20,0,10) \)
利用
\[
\tan\angle CAB = \frac{|\vec{AB} \times \vec{AC}|}{\vec{AB} \cdot \vec{AC}}
\]
計算得：
- 叉積長度 \( = 200\sqrt{6} \)
- 點積 \( = 400 \)
故
\[
\tan\angle CAB = \frac{200\sqrt{6}}{400} = \frac{\sqrt{6}}{2}
\]
**答：** \( \dfrac{\sqrt{6}}{2} \) 報錯
ChatGPT DeepSeek
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf
相關試題
