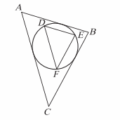
<選填>如圖,正三角形 \(ABC\) 的邊長為 1,並
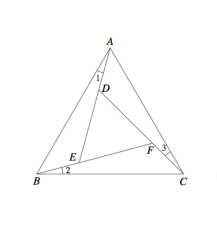且 \(\angle 1 = \angle 2 = \angle 3 = 15°\)。已知 \(\sin 15° = \frac{\sqrt{6} – \sqrt{2}}{4}\),則正三角形 \(DEF\) 的邊長為 __________。
在 \(\triangle ABE\) 中，
\[
\angle ABE = 60^\circ - 15^\circ = 45^\circ,\quad
\angle AEB = 180^\circ - 15^\circ - 45^\circ = 120^\circ.
\]
由正弦定理：
\[
\frac{AE}{\sin 45^\circ} = \frac{BE}{\sin 15^\circ} = \frac{AB}{\sin 120^\circ}
\]
其中 \(AB = 1\)，因此
\[
\frac{1}{\sin 120^\circ} = \frac{1}{\frac{\sqrt{3}}{2}} = \frac{2}{\sqrt{3}}.
\]
於是
\[
BE = \frac{\sin 15^\circ}{\sin 120^\circ} = \frac{\frac{\sqrt{6} - \sqrt{2}}{4}}{\frac{\sqrt{3}}{2}}
= \frac{\sqrt{6} - \sqrt{2}}{2\sqrt{3}},
\]
\[
AE = \frac{\sin 45^\circ}{\sin 120^\circ} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}
= \frac{\sqrt{2}}{\sqrt{3}}.
\]
由對稱性（\(\triangle ABE \cong \triangle CAD\)）得 \(AD = BE\)。
正三角形 \(DEF\) 的邊長為
\[
DE = AE - AD = \frac{\sqrt{2}}{\sqrt{3}} - \frac{\sqrt{6} - \sqrt{2}}{2\sqrt{3}}
= \frac{2\sqrt{2} - (\sqrt{6} - \sqrt{2})}{2\sqrt{3}}
= \frac{3\sqrt{2} - \sqrt{6}}{2\sqrt{3}}.
\]
有理化：
\[
\frac{3\sqrt{2} - \sqrt{6}}{2\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}
= \frac{3\sqrt{6} - 3\sqrt{2}}{6}
= \frac{\sqrt{6}}{2} - \frac{\sqrt{2}}{2}.
\]
故正三角形 \(DEF\) 的邊長為 \(\displaystyle \frac{\sqrt{6} - \sqrt{2}}{2}\)。
相關試題
