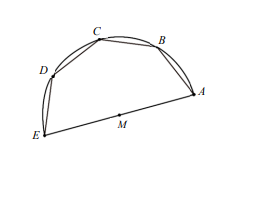
<多選>如圖,以 \(M\) 為圓心、\(MA = 8\) 為半徑畫圓,\(AE\) 為該圓的直徑,\(B\)、\(C\)、\(D\) 三點皆在圓上,且 \(AB = BC = CD = DE\)。若 \(MD = 8(\cos(\theta + 90^\circ), \sin(\theta + 90^\circ))\)。請選出正確的選項。
(1) \(MA = 8(\cos \theta, \sin \theta)\)
(2) \(MC = 8(\cos(\theta + 45^\circ), \sin(\theta + 45^\circ))\)
(3) (內積)\(MA \cdot MA = 8\)
(4) (內積)\(MB \cdot MD = 0\)
(5) \(BD = 8(\cos \theta + \cos(\theta + 90^\circ), \sin \theta + \sin(\theta + 90^\circ))\)
將圖形坐標化,令 \( M(0, 0) \),\( A(8, 0) \)。
由題意知 \( B, C, D \) 為弧 \( \overparen{AE} \) 的四等分點,
故 \( D(8\cos 135^\circ, 8\sin 135^\circ) \),即 \( \theta = 45^\circ \)。
(1) ×:\( \overrightarrow{MA} = (8, 0) \)
(2) ○:\( \overrightarrow{MC} = (0, 8) = (8\cos 90^\circ, 8\sin 90^\circ) \)
(3) ×:\( \overrightarrow{MA} \cdot \overrightarrow{MA} = 64 \)
(4) ○:\( \overrightarrow{MB} \perp \overrightarrow{MD} \Rightarrow \overrightarrow{MB} \cdot \overrightarrow{MD} = 0 \)
(5) ×:\( \overrightarrow{BD} = 8(\cos 135^\circ - \cos 45^\circ, \sin 135^\circ - \sin 45^\circ) \)
故選 (2)(4)