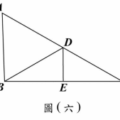
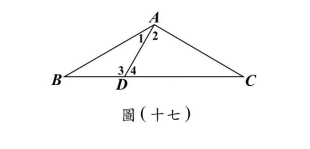
<非選擇題>如圖(十七),$\triangle ABC$中,$AB = AC$,$D$點在$BC$上,$\angle BAD = 30^\circ$,且$\angle ADC = 60^\circ$。請完整說明為何$AD = BD$與$CD = 2BD$的理由。
答案
(1)由外角定理得$\angle B = 30^\circ$,故$\triangle ABD$等腰,$AD=BD$。
(2)$\triangle ACD$為$30^\circ\text{-}60^\circ\text{-}90^\circ$,故$CD=2AD=2BD$。