105學測自然試題-41

---

<單選題>一物體的動量定義為質量與速度的乘積。假設甲、乙兩物體的質量分別為 \( m \) 與 \( m’ \)，此兩物體於 \( \Delta t \) 時段內發生正面碰撞，碰撞前後的速度變化量分別為 \( \Delta v \) 與 \( \Delta v’ \)。依據牛頓第二運動定律，在 \( \Delta t \) 時段內甲、乙的平均受力 \( F \) 與 \( F’ \) 分別為 \( F = m \frac{\Delta v}{\Delta t} \) 與 \( F’ = m’ \frac{\Delta v’}{\Delta t} \)，而根據牛頓第三運動定律 \( F = -F’ \)，故可得 \( m\Delta v + m’\Delta v’ = 0 \)，此即為「動量守恆律」。依據前述牛頓運動定律、動量守恆律，以及外力所作的功等於物體動能變化量的定理，回答下列41-43題有關碰撞的問題。
以高速攝影機拍攝一質量為50 g之網球撞擊牆面的過程，所得到的球中心速度 v 對時間 t 的變化如圖12所示，則在撞擊牆面的過程中，網球受到牆面平均作用力的量值，最接近下列何者？
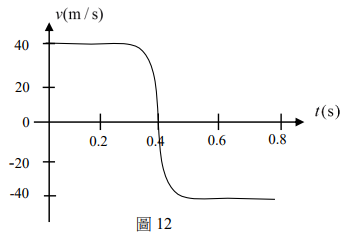
(A) 0.02N (B) 0.2N (C) 2N (D) 20N (E) 200N