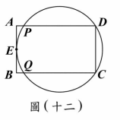
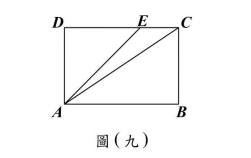
<單選題>圖(九)的矩形$ABCD$中，$E$點在$CD$上，且$AE \lt AC$。若$P$、$Q$兩點分別在$AD$、$AE$上，$AP : PD = 4 : 1$，$AQ : QE = 4 : 1$，直線$PQ$交$AC$於$R$點，且$Q$、$R$兩點到$CD$的距離分別為$q$、$r$，則下列關係何者正確？
(A) $q \lt r$，$QE = RC$
(B) $q \lt r$，$QE \lt RC$
(C) $q = r$，$QE = RC$
(D) $q = r$，$QE \lt RC$
答案
(D)
由比例得$PQ \parallel CD$，故$q = r$；又$QE = \frac{1}{5}AE$，$RC = \frac{1}{5}AC$，因$AE \lt AC$，故$QE \lt RC$。
相關試題
