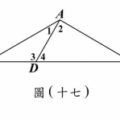
<單選題>如圖(十三),正六邊形$ABCDEF$中,$P$、$Q$兩點分別為$\triangle ACF$、$\triangle CEF$的內心。若$AF=2$,則$PQ$的長度為何?
 (A) $1$
(A) $1$(B) $2$
(C) $2\sqrt{3} – 2$
(D) $4 – 2\sqrt{3}$
答案
(C)
利用對稱性及$30^\circ\text{-}60^\circ\text{-}90^\circ$三角形內切圓半徑公式,得$PQ = 2(\sqrt{3} - 1) = 2\sqrt{3} - 2$。