<非選擇題>如圖(十八),正方形$ABCD$是一張邊長為$12$公分的皮革。皮雕師傅想在此皮革兩相鄰的角落分別切下$\triangle PDQ$與$\triangle PCR$後得到一個五邊形$PQABR$,其中$PD = 2DQ$,$RC = PC$,且$P$、$Q$、$R$三點分別在$CD$、$AD$、$BC$上,如圖(十八)所示。
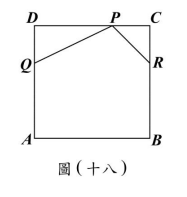
(1)當皮雕師傅切下$\triangle PDQ$時,若$DQ$長度為$x$公分,請你以$x$表示此時$\triangle PDQ$的面積。
(2)承(1),當$x$的值為多少時,五邊形$PQABR$的面積最大?請完整說明你的理由並求出答案。
答案
(1)$\triangle PDQ$面積$= \frac{1}{2} \cdot x \cdot 2x = x^2$。
(2)五邊形面積$= -3x^2 + 24x + 72 = -3(x-4)^2 + 120$,當$x=4$時最大。