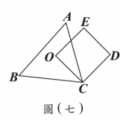
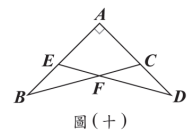
<單選題>如圖(十),$\triangle ABC$、$\triangle ADE$中,$C$、$E$兩點分別在$AD$、$AB$上,且$BC$與$DE$相交於$F$點。若$\angle A = 90^\circ$,$\angle B = \angle D = 30^\circ$,$AC = AE = 1$,則四邊形$AEFC$的周長為何?
(A) $2\sqrt{2}$
(B) $2\sqrt{3}$
(C) $2+\sqrt{2}$
(D) $2+\sqrt{3}$
答案
(B)
利用$30^\circ\text{-}60^\circ\text{-}90^\circ$三角形性質得$AB=\sqrt{3}$,$EF=CF=\sqrt{3}-1$,周長$=1+(\sqrt{3}-1)+(\sqrt{3}-1)+1=2\sqrt{3}$。