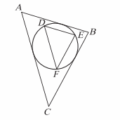
<選填題>如圖(此為示意圖),在\(\triangle ABC\)中,\(\overline{AD}\)交\(\overline{BC}\)於\(D\)點,\(\overline{BE}\)交\(\overline{AD}\)於\(E\)點,且\(\angle ACB = 30^\circ\),\(\angle EDB = 60^\circ\),\(\angle AEB = 120^\circ\)。若\(\overline{CD} = 15\),\(\overline{ED} = 7\),則\(\overline{AB} = \) __________。
答案
由角度關係可推\(\triangle BDE\)為正三角形,\(\overline{BE}=7\);\(\triangle ACD\)中,\(\angle ACD=30^\circ\),\(\angle ADC=120^\circ\),推得\(\overline{AD}=15\),故\(\overline{AE}=8\)。在\(\triangle ABE\)中,\(\angle AEB=120^\circ\),由餘弦定理:\(\overline{AB}^2 = 8^2+7^2-2\cdot8\cdot7\cdot\cos120^\circ = 64+49+56=169\),故\(\overline{AB}=13\)。答案:13