---

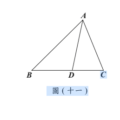
<單選題>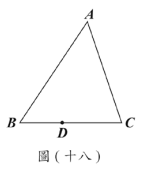圖(十八)在 $\triangle ABC$ 中，$\overline{AB} \gt \overline{AC} \gt \overline{BC}$，且 $D$ 為 $\overline{BC}$ 上一點。今打算在 $\overline{AB}$ 上找一點 $P$，在 $\overline{AC}$ 上找一點 $Q$，使得 $\triangle APQ$ 與 $\triangle PDQ$ 全等。以下是甲、乙兩人作法：
（甲） 連接 $\overline{AD}$，作 $\overline{AD}$ 的中垂線交 $\overline{AB}$、$\overline{AC}$ 於 $P$ 點、$Q$ 點，則 $P$、$Q$ 兩點即為所求。
（乙） 過 $D$ 作與 $\overline{AC}$ 平行的直線交 $\overline{AB}$ 於 $P$ 點；過 $D$ 作與 $\overline{AB}$ 平行的直線交 $\overline{AC}$ 於 $Q$ 點，則 $P$、$Q$ 兩點即為所求。
(A)兩人皆正確
(B)兩人皆錯誤
(C)甲正確，乙錯誤
(D)甲錯誤，乙正確