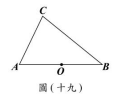
<單選題>如圖(十九),銳角三角形 $\triangle ABC$ 中,$O$ 點為 $\overline{AB}$ 的中點。
甲、乙兩人想在 $\overline{AC}$ 上找一點 $P$,使得 $\triangle ABP$ 的外心為 $O$,他們的作法分別如下:
(甲) 過 $B$ 作與 $\overline{AC}$ 垂直的直線,交 $\overline{AC}$ 於 $P$ 點,則 $P$ 即為所求。
(乙) 以 $O$ 為圓心,$\overline{OA}$ 為半徑畫弧,交 $\overline{AC}$ 於 $P$ 點,則 $P$ 即為所求。
對於甲、乙兩人的作法,下列判斷何者正確?
(A)兩人皆正確
(B)兩人皆錯誤
(C)甲正確,乙錯誤
(D)甲錯誤,乙正確
答案