<單選題>48-49為題組
如圖11所示，今有質量分別為\( m_{甲} \)與\( m_{乙} \)之甲、乙兩小球，其質量比值 \(\frac{m_{甲}}{m_{乙}} = \alpha < 1\)，將兩小球分別用長度為L的細線懸掛於同一固定點O，甲球靜止懸掛，而乙球向右拉直至細線呈現水平，然後靜止釋放乙球使其與甲球產生碰撞，且兩球立即黏在一起，黏在一起後濾起的最大高度為\( L/2 \)，圖12為其示意圖，細繩質量及空氣阻力均可忽略。
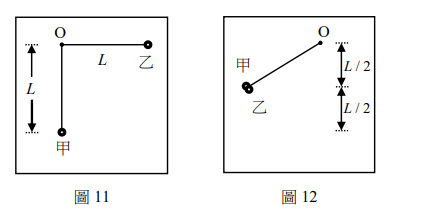
48. 假設以兩球自然下垂時的最低點為位能零點，則因碰撞而損失的力學能佔原來總力學能的比例為下列何者？
(A) \(\frac{1}{\alpha}\) (B) \(\frac{\alpha}{2}\) (C) \(\frac{1 – \alpha}{2}\) (D) \(\frac{1 + \alpha}{2}\) (E) 0
乙球原高位能：( m_B g L )。碰撞前乙球速度v：( frac{1}{2} m_B v^2 = m_B g L ) → ( v = sqrt{2gL} )。完全非彈性碰撞後共同速度V：( m_B v = (m_A + m_B) V ) → ( V = frac{m_B}{m_A + m_B} v )。碰撞後上升高度h：( frac{1}{2} (m_A+m_B) V^2 = (m_A+m_B) g h ) → ( h = frac{V^2}{2g} = frac{m_B^2}{(m_A+m_B)^2} frac{v^2}{2g} = frac{m_B^2}{(m_A+m_B)^2} L )。已知h=L/2。故 ( frac{m_B^2}{(m_A+m_B)^2} = frac{1}{2} ) → ( frac{m_B}{m_A+m_B} = frac{1}{sqrt{2}} ) → ( m_A + m_B = sqrt{2} m_B ) → ( m_A = (sqrt{2}-1) m_B ) → ( alpha = m_A/m_B = sqrt{2}-1 )。原總力學能E_i = m_B g L。碰撞後瞬間動能E_k' = frac{1}{2} (m_A+m_B) V^2 = (m_A+m_B) g h = (m_A+m_B) g (L/2)。損失能量ΔE = E_i - E_k' = m_B g L - frac{(m_A+m_B)}{2} g L = g L [ m_B - frac{m_A+m_B}{2} ] = g L [ frac{2m_B - m_A - m_B}{2} ] = g L [ frac{m_B - m_A}{2} ]。損失比例 = ΔE / E_i = [ (m_B - m_A)/2 ] / m_B = frac{1}{2} (1 - alpha)。答案(C) (frac{1 - alpha}{2})。 報錯
ChatGPT DeepSeek
相關試題
