<選填題>
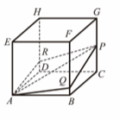
有一個三角形公園,其三頂點為 $O$、$A$、$B$,在頂點 $O$ 處有一座 150 公尺高的觀景台,某人站在觀景台上觀測地面上另兩個頂點 $A$、$B$ 與 $AB$ 的中點 $C$,測得其俯角分別為 $30^\circ$、$60^\circ$、$45^\circ$。則此三角形公園的面積為 【 】 平方公尺。(化成最簡根式)
答案
$7500\sqrt{2}$
設觀景台頂為 $H$,$HO=150$。由俯角得:$OA = 150/\tan30^\circ = 150\sqrt{3}$,$OB = 150/\tan60^\circ = 50\sqrt{3}$,$OC = 150/\tan45^\circ = 150$。在 $\triangle OAB$ 中,$C$ 為 $AB$ 中點,利用中線公式:$OC^2 = \frac{2OA^2 + 2OB^2 - AB^2}{4}$,代入解得 $AB^2 = 60000$。再由餘弦定理或向量法得 $\angle ABO = 90^\circ$,故面積 $= \frac{1}{2}\cdot OB\cdot AB = 7500\sqrt{2}$