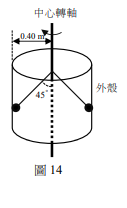
<非選擇題>二、調速器可用來控制馬達的轉速，其結構如圖14所示，圓筒狀的外殼固定不動，中心轉軸隨馬達旋轉，軸上兩側各有一質量可忽略的短棒，其上端與中心轉軸連接，下端各有一個質量為1.0kg的擺錘，兩短棒與中心轉軸按在同一平面，且此平面隨中心轉軸旋轉時，短棒可以自由張開或合攏，當張角為45°時，擺錘恰可觸及外殼；當轉速夠大時擺錘會貼著外殼，對外殼施力，以傳達馬達轉速過大的訊息。已知外殼的內半徑為0.40m，重力加速度g=10m/s\(^2\)。
1. 當擺錘恰可觸及外殼而不對外殼施力時，計算此時中心轉軸的角速度。（4分）
2. 當中心轉軸以角速度6rad/s旋轉時，計算任一擺錘對外殼施加的正向力量值。（3分）
3. 若擺錘和外殼間的動摩擦係數μ=0.25，當中心轉軸的角速度維持6rad/s時，計算任一擺錘因摩擦而損耗的功率。（3分）
略解：1. 擺錘恰觸外殼不受力時，張角 \( \theta = 45^\circ \)，半徑 \( r = 0.40 \text{m} \)。
受力分析：張力 \( T \)，重力 \( mg \)，向心力 \( m\omega^2 r \)。
\( T \cos\theta = mg \)，\( T \sin\theta = m\omega^2 r \)。
兩式相除得 \( \tan\theta = \frac{\omega^2 r}{g} \Rightarrow \omega = \sqrt{\frac{g \tan\theta}{r}} = \sqrt{\frac{10 \times \tan 45^\circ}{0.40}} = \sqrt{25} = 5 \text{rad/s} \)。
2. 當 \( \omega = 6 \text{rad/s} \gt 5 \text{rad/s} \)，擺錘貼外殼，設正向力 \( N \)。
水平：\( T\sin\theta + N = m\omega^2 r \)
鉛直：\( T\cos\theta = mg \)
由鉛直式 \( T = \frac{mg}{\cos\theta} \)，代入水平式：
\( \frac{mg}{\cos\theta} \sin\theta + N = m\omega^2 r \Rightarrow mg\tan\theta + N = m\omega^2 r \)
\( N = m(\omega^2 r - g\tan\theta) = 1.0 \times (6^2 \times 0.40 - 10 \times 1) = 1.0 \times (14.4 - 10) = 4.4 \text{N} \)。
3. 動摩擦力 \( f_k = \mu N = 0.25 \times 4.4 = 1.1 \text{N} \)。
擺錘線速度 \( v = \omega r = 6 \times 0.40 = 2.4 \text{m/s} \)。
摩擦損耗功率 \( P = f_k v = 1.1 \times 2.4 = 2.64 \text{W} \)。
答案：1. \( 5 \text{rad/s} \) 2. \( 4.4 \text{N} \) 3. \( 2.64 \text{W} \) 報錯
ChatGPT DeepSeek
相關試題
