<選擇題>
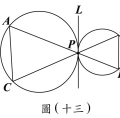
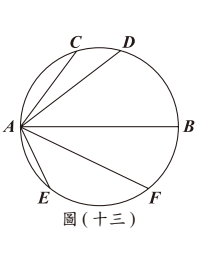有一直徑為 $AB$ 的圓，且圓上有 $C$、$D$、$E$、$F$ 四點，其位置如圖(十三)所示。若 $AC= 6$，$AD= 8$，$AE= 5$，$AF= 9$，$AB= 10$，則下列弧長關係何者正確？(A) $\overset{\frown}{AC}+ \overset{\frown}{AD}= \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF}= \overset{\frown}{AB}$
(B) $\overset{\frown}{AC}+ \overset{\frown}{AD}= \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF} \neq \overset{\frown}{AB}$
(C) $\overset{\frown}{AC}+ \overset{\frown}{AD} \neq \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF}= \overset{\frown}{AB}$
(D) $\overset{\frown}{AC}+ \overset{\frown}{AD} \neq \overset{\frown}{AB}$，$\overset{\frown}{AE}+ \overset{\frown}{AF} \neq \overset{\frown}{AB}$
答案
B
直徑所對圓周角為直角，弦長對應角度：$\sin(\theta/2)=\text{弦}/10$。計算得 $\angle AOC+\angle AOD=180^\circ$，但 $\angle AOE+\angle AOF\neq180^\circ$。
相關試題
