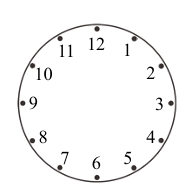
<多選>有一個依順時針方向依序標示1,2,…,12數字的圓形時鐘(如圖所示)。一開始在此時鐘「12」點鐘位置擺設一枚棋子,然後每次投擲一枚均勻銅板,依投擲
結果,照以下規則移動這枚棋子的位置:
● 若出現正面,將棋子從當時位置依順時針方向移動5個鐘點。
● 若出現反面,將棋子從當時位置依逆時針方向移動5個鐘點。
例如:若投擲銅板三次均為正面,則棋子第一次移動到「5」點鐘位置、第二次移動到「10」點鐘位置,第三次移動到「3」點鐘位置。
對任一正整數 \(n\),令隨機變數 \(X_n\) 代表依上述規則經過 \(n\) 次移動後棋子所在的點鐘位置,\(P(X_n = k)\) 代表 \(X_n = k\) 的機率(其中 \(k = 1,2,…,12\)),且令 \(E(X_n)\) 代表 \(X_n\) 的期望值。試選出正確的選項。
(1) \(E(X_1) = 6\)
(2) \(P(X_2 = 12) = \frac{1}{4}\)
(3) \(P(X_8 = 5) \geq \frac{1}{2^8}\)
(4) \(P(X_8 = 4) = P(X_8 = 8)\)
(5) \(E(X_8) \leq 7\)
(1):
第一次移動,正面到5,反面到7,概率各\(\frac{1}{2}\)。\(E(X_1) = \frac{5 + 7}{2} = 6\),正確。
(2):\(X_2 = 12\)的路徑:第一次正(到5),第二次反:\(5 - 5 = 0 \equiv 12 \ (\text{mod}\ 12)\)。第一次反(到7),第二次正:\(7 + 5 = 12\)。
共2種路徑,\(P(X_2 = 12) = 2 \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{2} \neq \frac{1}{4}\),錯誤。
(3)
$X_8不可能等於5,P(x_8=5)=0$
(4)
因為對稱 正確
(5)
分成$(+,-)=\overset{到4}{(8,0)},\overset{到6}{(7,1)},\overset{到8}{(6,2)},\overset{到10}{(5,3)},\overset{到12}{(4,4)},\overset{到2}{(3,5)},\overset{到4}{(2,6)},\overset{到6}{(1,7)},\overset{到8}{(0,8)}$來討論\\
錯誤