---

<單選題>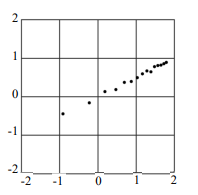某生推導出兩物理量 \( s \)，\( t \) 應滿足一等式。為了驗證其理論，他做了實驗得到15筆兩物理量的數據 \((s_k, t_k), k=1, \ldots, 15\) 。老師建議他將其中的 \( t_k \) 先取對數，在坐標平面上標出對應的點 \((s_k, \log t_k), k=1, \ldots, 15\) ，如右圖所示；其中第一個數據為橫軸坐標，第二個數據為縱軸坐標。利用迴歸直線分析，某生印證了其理論。
試問該生所得 \( s \)，\( t \) 的關係式最可能為下列哪一選項？
(1) $\quad s = 2t \quad$
(2) $\quad s = 3t \quad$
(3) $\quad t = 10^5$
(4) $\quad t^2 = 10^5 \quad$
(5) $\quad t^3 = 10^5$