---

<題組題>題組：第45題到第46題
臺灣西部海岸建構多部風力發電機,透過風力發電機可以將風能轉換為電能,而在轉換過程中,能量無法百分之百轉換｡科學上會使用功率係數 \(C_p\) 來呈現發電機葉片由風力獲取能量的效率,可表示如下:
\(C_p=\frac{發電機葉片由風力中獲取的功率}{通過發電機葉片風力原始的功率}\)
圖(一)為風力發電過程的示意圖,原始的風速為 \(v_1\),在通過發電機後,最後風速變為 \(v_2\),德國科學家貝茲通過理論計算,獲得理想情形下 \(C_p\) 與 \((\frac{v_2}{v_1})\) 的理論關係,其關係圖如圖(二)所示｡
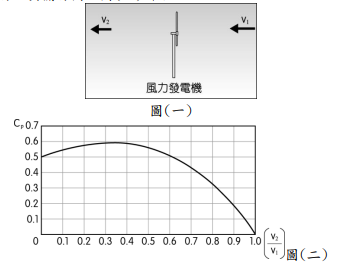
\(C_p\) 與 \(v_1\)、\(v_2\) 的關係式如下: \(C_p=\frac{1}{2}[1-(\frac{v_2}{v_1})^2][1+(\frac{v_2}{v_1})]\)
根據本文第一段的資訊,下列有關 \(C_p\) 的敘述,何者最合理?
(A)風力發電機葉片轉動的速率愈快, \(C_p\) 值會愈大
(B)風力發電機葉片轉動的速率愈快, \(C_p\) 值會愈小
(C)風力發電機葉片由風力獲得能量的比例愈高, \(C_p\) 值會愈大
(D)風力發電機葉片由風力獲得能量的比例愈高, \(C_p\) 值會愈小