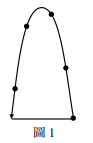
<單選題>某一雜技表演者用五顆相同的小球做單手拋球表演，由同一高度依次將各球略微偏離鉛直方向、向上拋出，當球回到原本被拋出的高度時，以同一隻手將球接住，然後水平移動到拋出點，再拋出，如圖1所示的逆時針軌跡。每次拋球的時間間隔固定為 \( \tau \)，初速的鉛直分量皆為 \( v_0 \)，各球的運動軌跡相同，形成連續的循環。過程中，在空中而不在手中的球至少有四顆。假設重力加速度的量值為 \( g \)，且空氣阻力可忽略，則下列選項何者正確？
(A) \( v_0 \) 可以是 \( \frac{g\tau}{2} \)
(B) \( v_0 \) 可以是 \( g\tau \)
(C) 每一小球在空中的時間可以是 \( 3\tau \)
(D) 小球在最高點時離拋出點的鉛直距離可以是 \( \frac{g\tau^2}{2} \)
(E) 小球在最高點時離拋出點的鉛直距離一定大於 \( 2g\tau^2 \)
答案
空中至少 4 顆球，故每球在空中時間 \( t \) 滿足 \( 4\tau < t < 5\tau \)。鉛直上拋 \( t = \frac{2v_0}{g} \)，故 \( 2g\tau < v_0 < \frac{5}{2}g\tau \)，(A)(B)錯。\( t \) 不在 \( 3\tau \) 範圍，(C)錯。最高點 \( h = \frac{v_0^2}{2g} = \frac{g}{2}(\frac{t}{2})^2 \)，代入 \( t \) 範圍得 \( 2g\tau^2 < h < \frac{25}{8}g\tau^2 \)，(D)錯(E)對。 報錯
ChatGPT DeepSeek
相關試題
