<單選題>
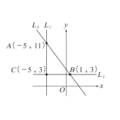
已知圓\(C: x^2 + (y-1)^2 = 10\)和直線\(L: 2x+y = c\)相交於相異兩點\(A\)、\(B\)。令\(O(0,1)\),當\(\triangle OAB\)面積有最大值時,所有可能的值之乘積為何?
(1) -6
(2) -12
(3) -18
(4) -24
(5) -30
答案
(4)
圓心\(K(0,1)\),半徑\(\sqrt{10}\)。設圓心到直線\(L\)的距離為\(d = \frac{|0+1-c|}{\sqrt{5}} = \frac{|1-c|}{\sqrt{5}}\)。弦長\(AB = 2\sqrt{10-d^2}\)。\(\triangle OAB\)面積為\(\frac{1}{2} \times AB \times d = d\sqrt{10-d^2}\)。由算幾不等式,當\(d^2 = 10-d^2\)即\(d=\sqrt{5}\)時面積最大。代入得\(\frac{|1-c|}{\sqrt{5}} = \sqrt{5} \Rightarrow |1-c|=5\),解得\(c=6\)或\(c=-4\),乘積為\(-24\)。