<選填題>
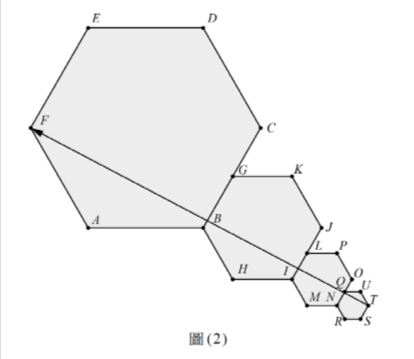圖(2)中有四個正六邊形，邊長由大至小分別為\(a_1\)、\(a_2\)、\(a_3\)、\(a_4\)，且滿足\(\frac{a_{n+1}}{a_n} = \frac{1}{2}, n=1,2,3\)。若\(\overset{\rightharpoonup}{TF} = x\overset{\rightharpoonup}{AB }+ y\overset{\rightharpoonup}{BC}\)，則數對\((x,y) = \underline{\quad }\)。
（化為最簡分數）
答案
\(\left( -\frac{15}{4}, \frac{7}{4} \right)\)
將\(\overrightarrow{TF}\)以\(\overrightarrow{AB}\)與\(\overrightarrow{AE}\)表示。利用正六邊形邊長比例關係，逐步分解路徑。計算得\(\overrightarrow{TF} = -\frac{23}{8}\overrightarrow{AB} + \frac{7}{8}\overrightarrow{AE}\)。再將\(\overrightarrow{AE}\)轉換為與\(\overrightarrow{BC}\)的關係（\(\overrightarrow{BC} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AE}\)），解得\(x = -15/4, y = 7/4\)。
相關試題
