<題組題>[題組:第18題到第20題]
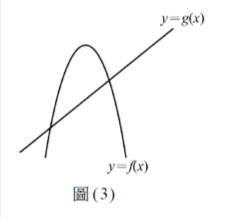
如圖(3)所示,坐標平面上,二次函數\(\Gamma: y = f(x) = a(x + 5)(x – k)\)與一次函數\(L: y = g(x) = m(x + 5)\)相交於\(A \sim B\)兩點,其中\(a \sim k\),\(m\)為實數。已知\(\Gamma\)的對稱軸為\(x = -2\),且\(A \sim B\)兩點分別在\(x\)、\(y\)軸上,設\(h(x) = f(x) \cdot g(x)\),試回答下列問題。
關於\(y = h(x)\),試選出正確的選項。(多選題,5分)
(1)\(y = h(x)\)的最高次項係數為負
(2)方程式\(h(x) = -1\)有三個相異實根
(3)\(y = h(x)\)經過適當平移可得\(y = amx^3\)的圖形
(4)\(y = h(x)\)圖形對稱中心的\(x\)坐標小於\(-2\)
(5)若\((x + 3)h(x)\)除以\(x + 1\)的餘式為 256,則\(a = -2\)
答案
(1)(4)(5)
由對稱軸\(x=-2\)及與\(L\)交點特性,可推得\(k=1, m=-a\),故\(h(x)=a(x+5)^2(x-1)(-a)= -a^2 (x+5)^2 (x-1)\)。
(1)三次項係數為\(-a^2 \lt 0\),對。
(2)\(h(x)=-1\)為三次方程,可能有1或3個實根,不一定有3相異實根,錯。
(3)圖形有因式\((x+5)^2\),非純三次方,錯。
(4)對稱中心\(x\)坐標為兩根平均\((-5-5+1)/3 = -3 \lt -2\),對。
(5)代入餘式定理計算可得\(a=-2\),對。

