<多選題>
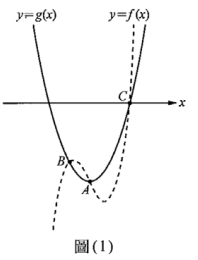已知三次函數\(y = f(x)\)與二次函數\(y = g(x)\)的圖形相交於\(A(3, -4), B, C\)三點，如圖(1)，其中\(A\)為\(y = f(x)\)圖形的對稱中心，也是\(y = g(x)\)圖形的頂點，且點\(C\)在\(x\)軸上，而兩多項式函數的領導係數皆為1。試選出正確的選項。(1) \(f(x) = (x-3)^3 – 4\)
(2) \(y = f(x)\)在\(x=3\)附近的一次近似直線斜率為\(-4\)
(3) 若\(f(x)\)除以\(g(x)\)的餘式為\(r(x)\)，則\(r(3) = -4\)
(4) \(y = f(x) – g(x)\)的圖形通過\(A, B, C\)三點
(5) 不等式\(f(x) \cdot g(x) \ge 0\)的解為\(x \ge 1\)
答案
(3)(5)
由條件設\(g(x)=(x-3)^2-4\)，且其一根為\(C(5,0)\)。設\(f(x)=(x-3)^3 + p(x-3) - 4\)，代入\(C(5,0)\)得\(p=-2\)，故\(f(x)=(x-3)^3 -2(x-3)-4\)。
(1)錯，此為嚴格遞增函數，與圖形(有轉折)不符。
(2)錯，一次近似（切線）斜率為\(f'(3)=p=-2\)。
(3)對，由餘式定理，\(r(3)=f(3)=-4\)。
(4)錯，\(f(x)-g(x)=0\)的根為交點的x坐標，但y坐標為0，並非原交點坐標。
(5)對，由圖形分析，當\(x\ge1\)時，\(f(x)\)與\(g(x)\)同號或至少其一為0。
相關試題
