---

<多選題>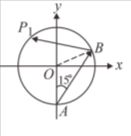在坐標平面上，\(O(0,0)\) 為原點，\(A(0,-1)\) 為單位圓上一點，試選出正確的選項。
(1)一質點由點 A 且沿著與 y 軸正向夾角為 15°的方向直線前進，經點 B 反射(即 \(\angle OBA = \angle OBP_1\))至圓上的點$ P_1$，再反射至圓上的點 $P_2$，如圖所示。如此連續進行 $n$ 次反射後會到圓上的點 $P_n$，則點 $P_{114}$ 的坐標為 \(\left(\frac{1}{2}, -\frac{\sqrt{3}}{2}\right)\)
(2)設 $n$ 為正整數，若點 $A$ 經矩陣 \(J = \left[\begin{array}{ccc}1 & 2 \\ 2 & -1\end{array}\right]\) 連續作線性變換 $n$ 次的對應點為 \(Q_n\left(x_n, y_n\right)\)，即\(J^n \left[\begin{array}{c}0 \\ -1\end{array}\right] = \left[\begin{array}{c}x_n \\ y_n\end{array}\right]\)，則滿足 \(Q_n Q_{n+1} \gt 2025\) 的最小正整數 $n$ 為 $8$
(3)設矩陣\(M_k = \begin{bmatrix}\cos \frac{k\pi}{180} & -\sin \frac{k\pi}{180} \\ \sin \frac{k\pi}{180} & \cos \frac{k\pi}{180}\end{bmatrix}, N_k = \begin{bmatrix}\cos \frac{k\pi}{180} & \sin \frac{k\pi}{180} \\ \sin \frac{k\pi}{180} & -\cos \frac{k\pi}{180}\end{bmatrix}, T = \begin{bmatrix}2 & -1 \\ 1 & 2\end{bmatrix}\)若單位圓上的動點 \( C(a,b) \) 在第一象限且 \(\frac{1}{2} \lt a \lt 1\)，點 \( C \) 經矩陣 \( M_1N_2 M_2 N_4 M_3 T \) 作線性變換的對應點為點 \( D \)，則點 \( D \) 的坐標可能為 \(\left( -\frac{3}{5}, \frac{4}{5} \right)\)
(4)設 \( J = \begin{bmatrix}1 & 2 \\ 2 & -1\end{bmatrix}, T = \begin{bmatrix}2 & -1 \\ 1 & 2\end{bmatrix}\)，若單位圓經矩陣 \( SJT \) 變換後的圖形為 \( \Gamma \)，則 \( O \) 點與 \( \Gamma \) 上的點之最長距離與最短距離的和為 $35$
(5)設 \( J = \begin{bmatrix}1 & 2 \\ 2 & -1\end{bmatrix}, T = \begin{bmatrix}2 & -1 \\ 1 & 2\end{bmatrix}, U = \begin{bmatrix}2 & 0 \\ 3 & 2\end{bmatrix}\)，若單位圓經矩陣 \( UJT \) 變換後的圖形為 \( \Omega \)，則 \( O \) 點與 \( \Omega \) 上的點之最長距離與最短距離的和為 $25$