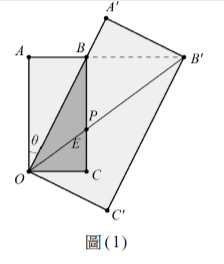
<單選題>圖(1)為兩相似矩形\(OABC\)、\(OA’B’C’\),其中\(O-B-A’\)且\(A-B-B’\)共線,對角線\(OB’\)交\(BC\)於\(P\)點。設\(OP=r\)且\(\angle AOB=\theta\),試選出線段\(A’B’\)的長。
(1)\(\frac{r\sin\theta}{\tan 2\theta}\)
(2)\(\frac{r\cos\theta}{\tan 2\theta}\)
(3)\(r\tan 2\theta \sin\theta\)
(4)\(r\tan 2\theta \cos\theta\)
(5)\(r\tan 2\theta \tan\theta\)
答案
(4)
在\(\triangle OBB'\)中,\(\angle OBB' = 90^\circ\),\(BB' = PB \cdot \tan 2\theta = r \tan 2\theta\)。在\(\triangle A'B'B\)中,\(\angle A'B'B = \theta\),故\(A'B' = BB' \cdot \cos\theta = r \tan 2\theta \cos\theta\)。