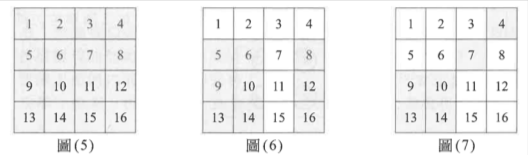
---

<多選題>娛樂節目正進行點燈遊戲，其規則如下：在 4×4 方陣內，每格放入編號 1~16 的燈泡，遊戲開始時所有燈泡皆熄滅，如圖(5)所示。當主持人隨機抽取一個號碼後，該號碼及該號碼之間行或同列燈泡，若原為熄燈狀態則點亮，若原為亮燈狀態則熄滅。舉例來說，當主持人抽中 3 號，則 1、2、3、4、7、11、15 號燈泡即亮燈，如圖(6)所示，維持此狀態下再抽中 8 號，則 5、6、8、12、16 號燈泡即亮燈；4、7 號燈泡即熄滅，如圖(7)所示。遊戲開始時，主持人依序隨機抽取 3 個相異號碼後，試選出正確的選項。(1)若主持人依序抽中 1、10，15，則 9 號澄泡為亮燈狀態
(2)若主持人依序抽中 5、11、13，則 9 號燈泡為熄滅狀態
(3)共有 $P_3^7$種方法，使得 9 號燈泡在遊戲過程中，先亮燈後又熄滅，最後又亮燈
(4)共有$P_1^7\times C_2^9$種方法，使得 9 號燈泡在主持人抽取第 1 個號碼亮燈後，維持亮燈狀態到最後
(5)共有 $1722$ 種方法數使 9 號燈泡最後為亮燈狀態