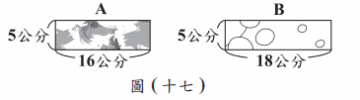
<非選擇題>
商店中販賣一款包含 A、B 兩種圖案的藝術紙片組合包，形狀分別為 16 公分×5 公分、18 公分×5 公分的長方形，如圖（十七）所示。
小燦打算在不裁切紙片的情況下，將這兩種藝術紙片以緊密相鄰的方式貼成圖（十八）的長方形，其中奇數層為 A 圖案，偶數層為 B 圖案，且最後一層為 A 圖案，而相同圖案的藝術紙片皆為相同的方向。
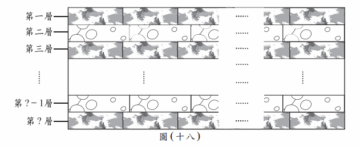
請根據上述資訊回答下列問題，完整寫出你的解題過程並詳細解釋：
(1) 以上述方式貼成的長方形，第一層最少有幾個 A 圖案？
(2) 已知每個組合包中 A、B 兩種圖案的藝術紙片數量比為 4：3，若小燦想購買一些組合包，貼成圖（十八）的長方形，其中第一層的 A 圖案數量與 (1) 求出之值相同，判斷他是否可能恰好把購買的藝術紙片用完？請說明理由。
(1) 設第一層有\( n \)個A圖案，總寬度為\( 16n \)公分
第二層B圖案數量需滿足\( 18m = 16n \)，即\( 9m = 8n \)
最小整數解：\( n = 9 \), \( m = 8 \)
(2) 設購買\( k \)個組合包，A紙片有\( 4k \)張，B紙片有\( 3k \)張
奇數層用A紙片，偶數層用B紙片，且最後一層為A
設有\( t \)層，則A紙片用量：\( \frac{t+1}{2} \times 9 \)，B紙片用量：\( \frac{t-1}{2} \times 8 \)
需滿足：\( \frac{t+1}{2} \times 9 = 4k \)，\( \frac{t-1}{2} \times 8 = 3k \)
解聯立得：\( t = 11 \), \( k = 12 \)
答案：(1) 9個 (2) 可能，當購買12個組合包時可貼成11層長方形 報錯
ChatGPT DeepSeek
相關試題
