複數極式的介紹

### 複數極式的介紹

複數極式（Polar Form of Complex Numbers）是一種表示複數的方式，它將複數從直角坐標系轉換到極坐標系，從而更直觀地描述複數的模（Magnitude）和幅角（Argument）。一個複數 \( z = a + bi \) 在直角坐標系中由實部 \( a \) 和虛部 \( b \) 表示，而在極坐標系中，複數可以表示為 \( z = r(\cos \theta + i \sin \theta) \)，其中 \( r = \sqrt{a^2 + b^2} \) 是複數的大小，代表複數到原點的距離；\( \theta = \tan^{-1}\left(\frac{b}{a}\right) \) 是複數的幅角，代表複數與實軸的夾角。

複數極式的一個重要應用是簡化複數的乘法和除法運算。例如，兩個複數 \( z_1 = r_1(\cos \theta_1 + i \sin \theta_1) \) 和 \( z_2 = r_2(\cos \theta_2 + i \sin \theta_2) \) 的乘積可以表示為 \( z_1 z_2 = r_1 r_2 [\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)] \)，這比直角坐標系中的運算更為簡潔。

此外，複數極式還廣泛應用於信號處理、電路分析、量子力學等領域。它不僅提供了一種更直觀的表示方法，還能揭示複數的幾何意義和物理意義。

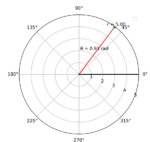
[複數極式圖示]以下圖展示了複數在直角坐標系和極坐標系中的表示方式：
圖中，複數 \( z = a + bi \) 在直角坐標系中的位置為 \( (a, b) \)，而在極坐標系中，其位置由大小 \( r \) 和幅角 \( \theta \) 確定。
這種轉換不僅方便計算，還為理解複數的性質提供了新的視角。