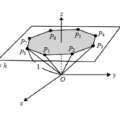
<單選題>坐標平面上，考慮\(A(2,3)\)與\(B(-1,3)\)兩點，並設\(O\)為原點。令\(E\)為滿足\(\overrightarrow{OP}=a\overrightarrow{OA}+b\overrightarrow{OB}\)的所有點\(P\)所形成的區域，其中\(-1\leq a\leq1\)，\(0\leq b\leq4\)。考慮函數\(f(x)=x^{2}+5\)，試問當限定\(x\)為區域\(E\)中的點\(P(x,y)\)的橫坐標時，\(f(x)\)的最大值為何？
(1)5
(2)9
(3)30
(4)41
(5)54
答案
已知\(\overrightarrow{OP}=a\overrightarrow{OA}+b\overrightarrow{OB}\)，\(\overrightarrow{OA}=(2,3)\)，\(\overrightarrow{OB}=(-1,3)\)，則\(\overrightarrow{OP}=(2a - b,3a + 3b)\)，所以\(x = 2a - b\)。
由\(-1\leq a\leq1\)，\(0\leq b\leq4\)，將\(x = 2a - b\)變形為\(b = 2a - x\)。
代入\(0\leq b\leq4\)，得到\(0\leq 2a - x\leq4\)。
當\(a = -1\)時，\(0\leq -2 - x\leq4\)，解得\(-6\leq x\leq -2\)；
當\(a = 1\)時，\(0\leq 2 - x\leq4\)，解得\(-2\leq x\leq2\) 。
所以\(x\)的取值範圍是\(-6\leq x\leq6\)。
對於二次函數\(f(x)=x^{2}+5\)，其二次項係數大於\(0\)，開口向上，在\(x\)的取值範圍\([-6,6]\)内，當\(x = 6\)或\(x = -6\)時，\(f(x)\)取得最大值，\(f(6)=6^{2}+5 = 41\)，\(f(-6)=(-6)^{2}+5 = 41\)。
答案為(4)。 報錯
ChatGPT DeepSeek
相關試題
