<選填題>坐標平面上有一梯形,四個頂點分別為 \( A(0,0),B(1,0),P,Q \),其中過 \( P,Q \) 兩點的直線方程式為 \( y=2x+4 \)。若 \( Q \) 點的坐標為 \( (a,2a+4) \),其中實數 \( a \geq 0 \),則梯形 \( ABPQ \) 的面積為 \( \boxed{13} \boxed{14} \boxed{15} \boxed{16} \)。(化為最簡分數)
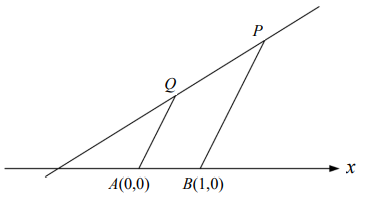
利用**相似三角形的面積比等於對應邊長的平方比**,分析\(\triangle CAQ\)與\(\triangle CBP\)的面積關係:
已知\(\triangle CAQ \sim \triangle CBP\),且對應邊長比\(\overline{CA}: \overline{CB} = 2: 3\),因此面積比為:
\[
\frac{\text{面積}(\triangle CAQ)}{\text{面積}(\triangle CBP)} = \left( \frac{\overline{CA}}{\overline{CB}} \right)^2 = \left( \frac{2}{3} \right)^2 = \frac{4}{9}
\]
接著計算\(\triangle CAQ\)與梯形\(ABPQ\)的面積比:
梯形\(ABPQ\)的面積 = \(\text{面積}(\triangle CBP) - \text{面積}(\triangle CAQ)\),因此:
\[
\frac{\text{面積}(\triangle CAQ)}{\text{面積}(\text{梯形}ABPQ)} = \frac{4}{9 - 4} = \frac{4}{5}
\]
再計算\(\triangle CAQ\)的面積:
已知\(\overline{CA} = 2\),\(\triangle CAQ\)的高為\(2a + 4\),由三角形面積公式得:
\[
\text{面積}(\triangle CAQ) = \frac{1}{2} \times \overline{CA} \times \text{高} = \frac{1}{2} \times 2 \times (2a + 4) = 2a + 4
\]
最後求梯形\(ABPQ\)的面積:
由面積比\(\frac{4}{5}\),可得:
\[
\text{面積}(\text{梯形}ABPQ) = \frac{5}{4} \times \text{面積}(\triangle CAQ) = \frac{5}{4} \times (2a + 4) = \frac{5}{2}a + 5
\]