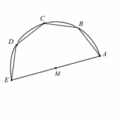
<題組題>[題組:第18-20題]坐標平面上O為原點,給定 \(A(1, 0) \cdot B(-2, 0)\) 兩點。另有兩點P、Q在上半平面,且滿足 \(AP = OA \cdot BQ = OB \cdot PQQ\) 為直角,如右圖所示。令∠AOP = θ。根據上述,試回答下列問題。

18. 線段 \(OP\) 長為下列哪一選項?(單選題,3分)
(1) \(\sin \theta\)
(2) \(\cos \theta\)
(3) \(2\sin \theta\)
(4) \(2\cos \theta\)
(5) \(\cos 2\theta\)
[題組:第18-20題]19. 若 \(\sin \theta = \frac{3}{5}\),試求點 \( Q \) 的坐標,並說明 \( BQ = 2AP \)。 (非選擇題,6分)
[題組:第18-20題]20. (承19.題) 試求點A到直線BQ的距離,並求四邊形PABQ的面積。(非選擇題,6分)
取 \( OP \) 中點 \( M \),由 \( OA = AP \) 且 \( AM \perp OP \) 可得 \( OP = 2OM = 2 \cos \theta \)
故選(4),取 \( OP \) 中點 \( M \),由 \( OA = AP \) 且 \( AM \perp OP \) 可得 \( OP = 2OM = 2 \cos \theta \)
故選(4)
\( \sin \theta = \frac{3}{5} \), \( \cos \theta = \frac{4}{5} \)
\( AP = (\cos 2\theta, \sin 2\theta) = (2\cos^2\theta - 1, 2\sin\theta\cos\theta) = (\frac{7}{25}, \frac{24}{25}) \)
\( BQ = 2AP = (\frac{14}{25}, \frac{48}{25}) \)
點 \( Q \) 坐標為 \( (-2 + \frac{14}{25}, \frac{48}{25}) = (-\frac{36}{25}, \frac{48}{25}) \)
\( \overrightarrow{BQ} = (\frac{14}{25}, \frac{48}{25}) // (7, 24) \),直線 \( BQ \) 方程式:\( 24x - 7y = -48 \)
點 \( A(1,0) \) 到直線距離 \( d = \frac{|24 \times 1 - 7 \times 0 + 48|}{\sqrt{24^2+(-7)^2}} = \frac{72}{25} \)
四邊形PABQ為梯形,面積 = \( \frac{(AP+BQ) \times d}{2} = \frac{(1+2) \times \frac{72}{25}}{2} = \frac{108}{25} \)
設 \( B(a,b) \),由 \( B \) 在 \( x^2+y^2=4 \) 上且 \( \overline{AB}=1 \),得 \( a^2+b^2=4 \), \( (a-\sqrt{3})^2+b^2=1 \)
相減得 \( 2\sqrt{3}a - 3 = 3 \Rightarrow a=\sqrt{3} \),代入得 \( b=1 \)
故選(4)
設 \( A'(c,d) \),由 \( A' \) 在 \( x^2+y^2=3 \) 上且 \( \overline{A'B'}=1 \),得 \( c^2+d^2=3 \), \( (c+2)^2+d^2=1 \)
相減得 \( 4c+4=-2 \Rightarrow c=-\frac{3}{2} \),代入得 \( d=\frac{\sqrt{3}}{2} \)
∴ \( A' \left( -\frac{3}{2}, \frac{\sqrt{3}}{2} \right) \),極坐標 \( \left[ \sqrt{3}, \frac{5\pi}{6} \right] \)
\( \cos \angle OA'B' = \frac{\overset{\rightharpoonup}{A'O} \cdot \overset{\rightharpoonup}{A'B'}}{|\overset{\rightharpoonup}{A'O}||\overset{\rightharpoonup}{A'B'}|} = 0 \)
\( \Omega \) 面積 = 扇形 \( OBD \) 面積 + \( \triangle OAB \) 面積 - 扇形 \( OAC \) 面積
= \( \frac{1}{2} \times 4 \times \frac{\pi}{3} + \frac{1}{2} \times \sqrt{3} \times 1 - \frac{1}{2} \times 3 \times \frac{\pi}{2} = \frac{\sqrt{3}}{2} - \frac{\pi}{12} \)
\( R \) 面積 = \( \Omega \) 面積 + 第二象限掃過區域面積 = \( \left( \frac{\sqrt{3}}{2} - \frac{\pi}{12} \right) + \left( \frac{\pi}{2} - \frac{\sqrt{3}}{2} \right) = \frac{5\pi}{12} \)
美國大平原地區過度深耕翻土,破壞土壤結構,加劇沙塵暴。
答案:C
災民移往加州等西部地區,屬地中海型氣候,夏乾冬雨。
答案:B
受災區為美國大平原,屬溫帶草原景觀。
答案:B
美國大平原地區過度深耕翻土,破壞土壤結構,加劇沙塵暴。
答案:C
災民移往加州等西部地區,屬地中海型氣候,夏乾冬雨。
答案:B
受災區為美國大平原,屬溫帶草原景觀。
答案:B