<單選題>
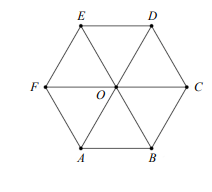
如圖所示,\(O\)為正六邊形之中心。試問下列哪個向量的終點P落在\(\triangle ODE\)內部(不含邊界)?
(1) \(\overset{\rightharpoonup}{OP} = \overset{\rightharpoonup}{OC} + \overset{\rightharpoonup}{OE}\)
(2) \(\overset{\rightharpoonup}{OP} = \frac{1}{4} \overset{\rightharpoonup}{OC} + \frac{1}{2} \overset{\rightharpoonup}{OE}\)
(3) \(\overset{\rightharpoonup}{OP} = -\frac{1}{4} \overset{\rightharpoonup}{OC} + \frac{1}{2} \overset{\rightharpoonup}{OE}\)
(4) \(\overset{\rightharpoonup}{OP} = \frac{1}{4} \overset{\rightharpoonup}{OC} – \frac{1}{2} \overset{\rightharpoonup}{OE}\)
(5) \(\overset{\rightharpoonup}{OP} = -\frac{1}{4} \overset{\rightharpoonup}{OC} – \frac{1}{2} \overset{\rightharpoonup}{OE}\)。