<選填>如下圖,在坐標空間中,\(A, B, C, D, E, F, G, H\) 為
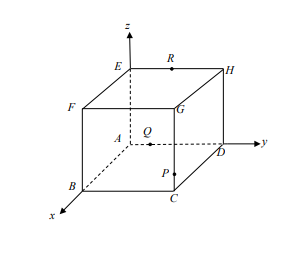正立方體的八個頂點,已知其中四個點的坐標 \(A(0, 0, 0)\)、\(B(6, 0, 0)\)、\(D(0, 6, 0)\) 及 \(E(0, 0, 6)\),\(P\) 在線段 \(CG\) 上且 \(CP : PG = 1 : 5\),\(R\) 在線段 \(EH\) 上且 \(ER : RH = 1 : 1\),\(Q\) 在線段 \(AD\) 上。若空間中通過 \(P, Q, R\) 這三點的平面,與直線 \(AG\) 不相交,則 \(Q\) 點的 \(y\) 坐標為___________。
由題意畫得知 \( A(0, 0, 0) \)、\( G(6, 6, 6) \)、\( P(6, 6, 1) \)、\( R(0, 3, 6) \)
設 \( Q(0, k, 0) \)
\[
\overrightarrow{PQ} = Q - P = (-6,\; k-6,\; -1)
\]
\[
\overrightarrow{PR} = R - P = (-6,\; -3,\; 5)
\]
平面 \( PQR \) 的法向量
\[
\overrightarrow{n} = \overrightarrow{PQ} \times \overrightarrow{PR}
\]
\[
= \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
-6 & k-6 & -1 \\
-6 & -3 & 5
\end{vmatrix}
\]
\[
= \mathbf{i} \begin{vmatrix} k-6 & -1 \\ -3 & 5 \end{vmatrix}
-\mathbf{j} \begin{vmatrix} -6 & -1 \\ -6 & 5 \end{vmatrix}
+\mathbf{k} \begin{vmatrix} -6 & k-6 \\ -6 & -3 \end{vmatrix}
\]
\[
= \mathbf{i}\big(5(k-6) - 3\big)
-\mathbf{j}\big((-6)\cdot5 - (-1)(-6)\big)
+\mathbf{k}\big((-6)(-3) - (k-6)(-6)\big)
\]
\[
= (5k - 30 - 3,\; -(-30 - 6),\; 18 + 6k - 36)
\]
\[
= (5k - 33,\; 36,\; 6k - 18)
\]
直線 \( AG \) 的方向向量 \(\overrightarrow{v}\) 平行於 \(\overrightarrow{AG} = (6, 6, 6)\)，可取 \(\overrightarrow{v} = (1, 1, 1)\)
若平面 \( PQR \) 與直線 \( AG \) 不相交，則
\[
\overrightarrow{n} \perp \overrightarrow{v} \quad\Rightarrow\quad \overrightarrow{n} \cdot \overrightarrow{v} = 0
\]
\[
(5k - 33) \cdot 1 + 36 \cdot 1 + (6k - 18) \cdot 1 = 0
\]
\[
5k - 33 + 36 + 6k - 18 = 0
\]
\[
11k - 15 = 0
\]
\[
\therefore k = \frac{15}{11}
\]
相關試題
