<選填>小鎮 \(A\) 距離一筆直道路 6 公里,並與道路上的小鎮 \(B\) 相距 12 公里。今欲在此道路上蓋一家超級市場使其與 \(A, B\) 等距,則此超級市場與 \(A\) 的距離須為__________ 公里。
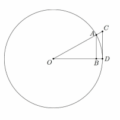
設超級市場位置為 \( P \),滿足 \( PA = PB = x \)(公里),如圖所示。
\( H \) 為 \( AB \) 中點,則 \( AH = HB = \frac{12}{2} = 6 \)。
在 \(\triangle ABH\) 中,由畢氏定理得:
\[
HB = \sqrt{AB^2 - AH^2} = \sqrt{12^2 - 6^2} = \sqrt{144 - 36} = \sqrt{108} = 6\sqrt{3}。
\]
設 \( HP = y \),則 \( HB = HP + PB \) 即:
\[
6\sqrt{3} = y + x \quad \Rightarrow \quad y = 6\sqrt{3} - x。
\]
在 \(\triangle AHP\) 中,再由畢氏定理得:
\[
AP^2 = AH^2 + HP^2,
\]
\[
x^2 = 6^2 + \left(6\sqrt{3} - x\right)^2。
\]
展開:
\[
x^2 = 36 + \left(108 - 12\sqrt{3}x + x^2\right)。
\]
兩邊消去 \( x^2 \):
\[
0 = 36 + 108 - 12\sqrt{3}x。
\]
\[
12\sqrt{3}x = 144。
\]
\[
x = \frac{144}{12\sqrt{3}} = \frac{12}{\sqrt{3}} = \frac{12\sqrt{3}}{3} = 4\sqrt{3}。
\]
故超市與 \( A \) 點的距離為 \( 4\sqrt{3} \) 公里。