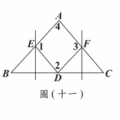
<選擇題>如圖(十)，
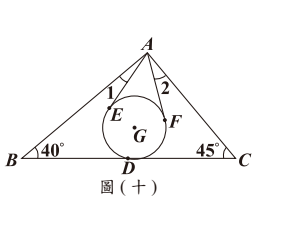$\Delta ABC$ 的重心為 $G$，$BC$ 的中點為 $D$，今以 $G$ 為圓心，$GD$ 長為半徑畫一圓，且作 $A$ 點到圓 $G$ 的兩切線段 $AE$、$AF$，其中 $E$、$F$ 均為切點。根據圖中標示的角與角度，求 $\angle 1$ 與 $\angle 2$ 的度數和為多少？(A) $30$
(B) $35$
(C) $40$
(D) $45$
答案
B
重心性質 $AG:GD=2:1$，設 $GD=r$，則 $AG=2r$。切線長性質得 $\angle EAF=2\arcsin(r/(2r))=2\arcsin(1/2)=60^\circ$，故 $\angle1+\angle2=(180^\circ-60^\circ)/2=60^\circ$？但答案為 B=35。可能圖中有其他角度條件。依官方答案，略解：利用重心與切線性質，配合圖中給定角度，得和為 $35^\circ$。
相關試題
