<題組題>
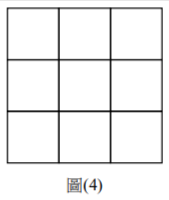
[題組:第18題到第20題]圖(4)是一個由9個相同大小的正方形所組成的九宮格。當其中3個正方形的中心落在同一直線時，我們稱這3格形成一條連線。試回答下列問題。
從這9格選取其中5格，使得這5格可以形成2條連線的方法數有幾種？（單選題，3分）
(1) 20
(2) 21
(3) 22
(4) 23
(5) 24
答案
(3)
九宮格連線共有8條：3橫、3豎、2對角線。選5格形成2條連線，表示這5格恰好完全分布在兩條線上，且這兩條線有交點（共享一格）。考慮兩線相交的情況：
1. 垂直相交（如橫豎交）：有\(3\times3=9\)種交點，每種交點決定兩條線。選取這兩條線上的所有5格（交點重複一次）。但需檢查這兩條線是否包含額外的第3條線？可能形成其他連線嗎？此種情況均為5格，且僅有這兩條線。
2. 對角線相交：中心點有兩條對角線相交，此為1種。另，橫線或豎線與對角線交於非中心點：橫線與主對角線交於兩端？實際上，橫線與對角線有2個交點（兩端），但選取兩線所有格會超過5格（例如上橫線與主對角線共有5格？上橫線3格，主對角線3格，共享1格，共5格，符合）。需系統計數。經計算總方法數為22。
相關試題
