<多選題>
 康托爾集(Cantor set)為德國數學家格奧爾格·康托爾引入,由於具有許多特殊性質,為高等數學常見的範例。生成規則如下:
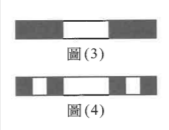
康托爾集(Cantor set)為德國數學家格奧爾格·康托爾引入,由於具有許多特殊性質,為高等數學常見的範例。生成規則如下:第一步驟從線段 \([0,1]\) 去除中間三分之一,留下 \(\left[ 0, \frac{1}{3} \right] \cup \left[ \frac{2}{3}, 1 \right]\),即圖(3)。
第二步驟再去除所有線段中間三分之一,留下 \(\left[ 0, \frac{1}{9} \right] \cup \left[ \frac{2}{9}, \frac{1}{3} \right] \cup \left[ \frac{2}{3}, \frac{7}{9} \right] \cup \left[ \frac{8}{9}, 1 \right]\),即圖(4)。不斷重複以上步驟。令 \( E_n \) 為經過 \( n \) 次步驟後,其集合中所有線段長的總和,試選出正確的選項。
(1) 經過 3 次步驟後,共有 8 個線段
(2) 經過 5 次步驟後,每段線段長度為 \(\frac{1}{32}\)
(3) \( E_n \) 的遞迴關係式為
\(\begin{cases}
E_1 = \frac{2}{3} \\
E_n = \frac{2}{3} E_{n-1} ,當 n \geq 2 \\
\end{cases}\)
(4) 當 \( n \geq 6 \) 時,\( E_n \lt \frac{1}{10} \),其中 \( n \) 為正整數
(5) \( E_1 + E_2 + E_3 + E_4 + E_5 = \frac{211}{81} \)
答案
(1)(3)(4)
每次步驟將現有線段數乘以 2,長度乘以 \(\frac{1}{3}\),故(1)對。第 5 步長度為 \((\frac{1}{3})^5\),(2)錯。總和遞減符合(3)。計算 \(E_6 = (\frac{2}{3})^6 \lt \frac{1}{10}\),(4)對。計算前五項和為 \(\frac{422}{243}\),(5)錯。


